代码如下

package main import ( "fmt" ) type Node struct { Value string Left, Right *Node } func (node *Node) Print() { fmt.Print(node.Value, " ") } func (node *Node) SetValue(v string) { if node == nil { fmt.Println("setting value to nil.node ignored.") return } node.Value = v } //前序遍历 func (node *Node) PreOrder() { if node == nil { return } node.Print() node.Left.PreOrder() node.Right.PreOrder() } //中序遍历 func (node *Node) MiddleOrder() { if node == nil { return } node.Left.MiddleOrder() node.Print() node.Right.MiddleOrder() } //后序遍历 func (node *Node) PostOrder() { if node == nil { return } node.Left.PostOrder() node.Right.PostOrder() node.Print() } //层次遍历(广度优先遍历) func (node *Node) BreadthFirstSearch() { if node == nil { return } result := []string{} nodes := []*Node{node} for len(nodes) > 0 { curNode := nodes[0] nodes = nodes[1:] result = append(result, curNode.Value) if curNode.Left != nil { nodes = append(nodes, curNode.Left) } if curNode.Right != nil { nodes = append(nodes, curNode.Right) } } for _, v := range result { fmt.Print(v, " ") } } //层数(递归实现) //对任意一个子树的根节点来说，它的深度=左右子树深度的最大值+1 func (node *Node) Layers() int { if node == nil { return 0 } leftLayers := node.Left.Layers() rightLayers := node.Right.Layers() if leftLayers > rightLayers { return leftLayers + 1 } else { return rightLayers + 1 } } //层数(非递归实现) //借助队列，在进行按层遍历时，记录遍历的层数即可 func (node *Node) LayersByQueue() int { if node == nil { return 0 } layers := 0 nodes := []*Node{node} for len(nodes) > 0 { layers++ size := len(nodes) //每层的节点数 count := 0 for count < size { count++ curNode := nodes[0] nodes = nodes[1:] if curNode.Left != nil { nodes = append(nodes, curNode.Left) } if curNode.Right != nil { nodes = append(nodes, curNode.Right) } } } return layers } func CreateNode(v string) *Node { return &Node{Value: v} } func main() { root := Node{Value: "A"} root.Left = &Node{} root.Left.SetValue("B") root.Left.Right = CreateNode("C") root.Right = &Node{"D", nil, nil} root.Right.Left = CreateNode("E") fmt.Print("\n前序遍历: ") root.PreOrder() fmt.Print("\n中序遍历: ") root.MiddleOrder() fmt.Print("\n后序遍历: ") root.PostOrder() fmt.Print("\n层次遍历: ") root.BreadthFirstSearch() fmt.Println("\n层数: ", root.Layers()) fmt.Println("\n层数: ", root.LayersByQueue())} ``` **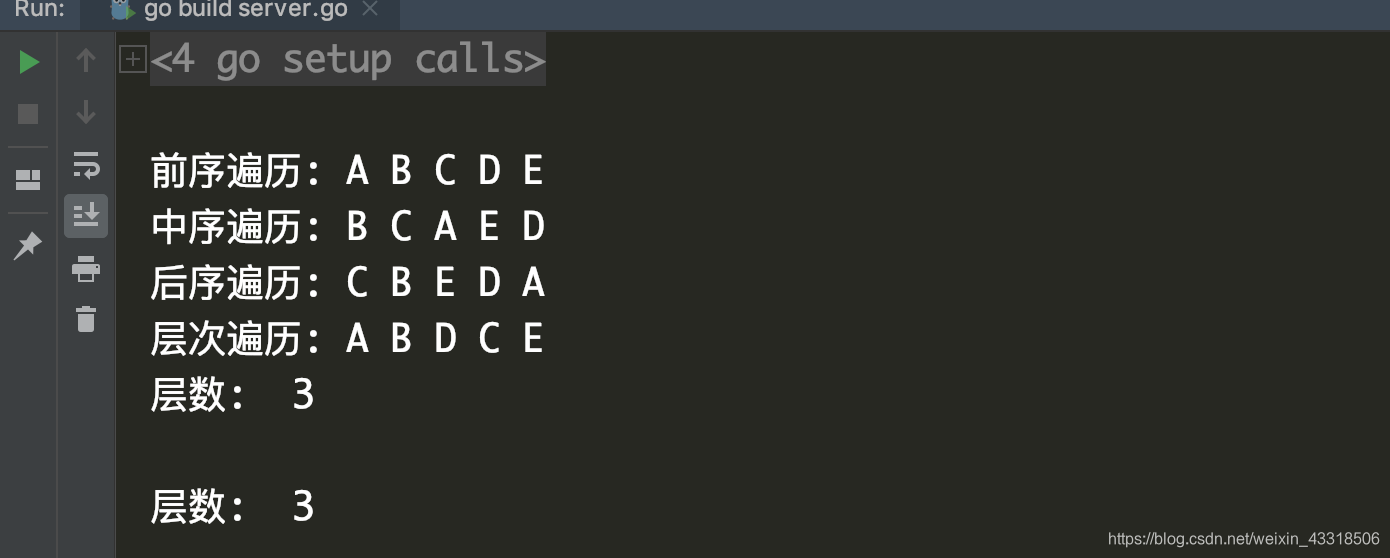结果如下：**